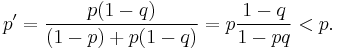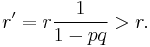Bayesian search theory

Bayesian search theory is the application of Bayesian statistics to the search for lost objects. It has been used several times to find lost sea vessels, for example the USS Scorpion.

Contents

Procedure

The usual procedure is as follows:

  1. Formulate a number of hypotheses about what happened to the vessel.
  2. Corresponding to each hypothesis construct a probability distribution for the location of the vessel
  3. Construct a probability distribution for actually finding an object in location X if it really is in location X. In an ocean search, this is usually a function of water depth — in shallow water chances of finding an object are good if the search is in the right place. In deep water chances are reduced.
  4. Combine the above information coherently to produce an overall probability distribution. (Usually this simply means multiplying the two distributions together.) This gives the probability of finding the vessel by looking in location X, for all possible locations X. (This is like a contour map of probability.)
  5. Construct a search path which starts at the point of highest probability and 'scans' over high probability areas, then intermediate probabilities, and finally low probability areas.
  6. Revise all the probabilities continuously during the search. For example, if the search of location X has yielded nothing then the probability that the vessel is there is greatly reduced (though not usually to zero) and the probabilities of all other locations must be increased. The revision process is done using Bayes' theorem.

The advantages of the Bayesian method are that all information available is used coherently (i.e. in a "leak-proof" manner) and the method automatically produces estimates of the cost for a given success probability. That is, even before the start of searching, one can say, hypothetically, "there is a 65% chance of finding it in a 5-day search. That probability will rise to 90% after a 10-day search and 97% after 15 days" or a similar statement. Thus the economic viability of the search can be estimated before committing resources to a search.

Apart from the USS Scorpion, other vessels located by Bayesian search theory include the MV Derbyshire, the largest British vessel ever lost at sea, and the SS Central America. It also proved successful in the search for a lost hydrogen bomb following the 1966 Palomares B-52 crash in Spain.

Bayesian search theory is incorporated into the CASP (Computer Assisted Search Program) mission planning software used by the United States Coast Guard for search and rescue. This program was later adapted for inland search by adding terrain and ground cover factors for use by the United States Air Force and Civil Air Patrol.

Mathematics

Suppose a grid square has a probability p of containing the wreck and that the probability of successfully detecting the wreck if it is there is q. If the square is searched and no wreck is found, then, by Bayes' theorem, the revised probability of the wreck being in the square is given by

p' = \frac{p(1-q)}{(1-p)%2Bp(1-q)} = p \frac{1-q}{1-pq} < p.

For each other grid square, if its prior probability is r, its posterior probability is given by

r' = r \frac{1}{1- pq} > r.

See also

References